Heaters in Series and Parallel
Electric Heating elements can be connected to a voltage source in a variety of different ways. Making sure things are done correctly is important so that you get the performance expected and, most importantly, to make sure it’s done safely.
If you have a 240V power supply but only 120V heaters available, are you able to use them? Why do people prefer heaters connected in series while others prefer them connected in parallel? What’s the difference? Are any special considerations required? We’ll cover those topics and more in this article.
When connecting electric heaters in series, they are all placed end-to-end along a single path, electrically, meaning the same current flows through each heater; whereas, in parallel, the heaters are connected with each heater across the voltage source so that the current splits and passes through the heaters separately, with each component experiencing the same voltage.

Key differences
Current flow:
In a series circuit, the current is the same through every heater, while in a parallel circuit, the current is divided among the different heaters.
Voltage distribution:
In a series circuit, the voltage is divided across each heater depending on their individual resistance, while in a parallel circuit, the voltage is the same across all heaters regardless of their individual resistance.
Put another way...
In series, the current through each heater is the same. The voltage drop across each one depends on its resistance. In parallel, the voltage drop across each heater is the same. The current through each one depends on its resistance.
Circuit failure:
If one heater in a series circuit fails, the entire circuit stops working, whereas in a parallel circuit, the remaining unfailed heaters continue to operate.
Now, some more details…
When heaters are connected in series, they are connected such that the current that flows through one heater flows through every heater that is connected in series with it. If you think of electrical flow as water in a pipe, the heaters, when connected end to end (like piping) have whatever water flows through one of them, flow through all of them. In this type of connection, if the resistance of each heater is the same, then the voltage drop across each heater is the same. If the resistances are different, the voltage drops are different.
The resistance of heaters connected in series is the sum of the individual heater resistances.
Example:
10Ω, 20Ω and 40Ω heaters connected in series have a total resistance of 10Ω + 20Ω + 40Ω = 70Ω.
Two heaters in Series
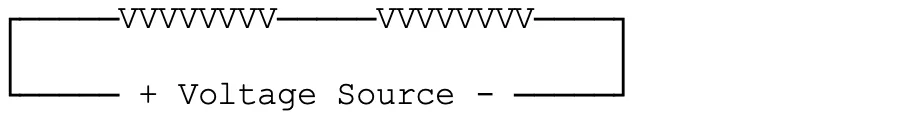
Three heaters in Series
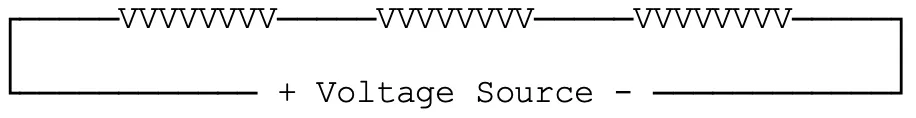
In these diagrams, “VVVVVVVV” is used to represent the resistance of each individual heater.
Here are a few additional examples.
For simple one: Let’s say you have 4 heaters connected in series, all rated at 100 watts when 120 volts is applied. If you apply 480 volts across those 4 heaters, the voltage drop across each one is 120 volts (480V / 4) and each one produces 100 watts. You’ve just made use of 4 heaters rated for 120 volts in a 480 volt power system. The drawback to that scenario is that you’ve got to make sure all the heaters can handle a 480V potential between the circuit and sheath; make sure the heaters’ dielectric strength is sufficient. Even though each heater ‘acts’ as if they only ‘see’ 120 volts, the entire system, heaters and all, must withstand the 480V force trying to break through the internal insulating material of the heater. If you had 3/16” diameter cartridge heaters it would not be recommend doing this in a 480V scenario due the heater’s small size and low dielectric strength. If you had 3/4” diameter heaters you would probably be fine.
For a more difficult example, if you had one 100W/120V heater and two 100W/240V heaters in that scenario things would behave quite differently. First you would need to calculate the resistance for each heater and determine the wattage produced by each of those heaters knowing that the current passing through each one is the same. In this case you would have 120²/100Ω, 240²/100Ω and 240²/100Ω of resistance in series or 144Ω, 576Ω and 576Ω. That’s a total of 1296Ω. 480V is being applied, so the total power output of the system will be 480²/1296 or 177.77 watts. With 177.77 watts of power being produced at 480V, that means there’s 177.77/480 or 0.37037 amps of current passing through all the heaters. Power is calculated as I²R so the power for each heater (in order) is 0.37037² x 144, 0.37037² x 576, and 0.37037² x 576. That gives the wattages of 19.75 watts, 79.01 watts and 79.01 watts, or a grand total of 177.77 watts. That’s good because it matches the overall number that was calculated earlier. For the voltage drop across each heater, and being that we know a lot about the condition of the situation, it can be calculated using RxI or P/I or √(PxR). For the first heater RxI = 144 x 0.37037 = 53.3V and P/I = 19.75 / 0.37037 = 53.3V and √(19.75 x 144) = 53.3V. It’s left to the reader to show that the voltage drop across the other two heaters is 213.3V each.
As stated earlier, if one of the heaters fails then the circuit is broken and all the heaters stop working. This is sometimes desirable because then you can tell if a single heater has failed and the system isn’t limping along with fewer heaters than intended.
If you’re into this sort of thing, here’s is the formula for determining the total resistance of a system of heaters that are connected in series. If you have n heaters connected in series, their total resistance, regardless of if they’re the same or not is:
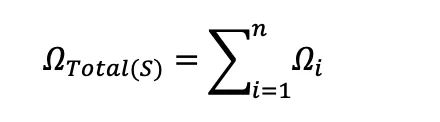
where:
ΩTotal(S) is the total resistance of heaters (n heaters) connected in series.
Σ is the capital Greek letter Sigma, meaning that everything to the right of it is summed
Ωi is the resistance of each individual heater, numbered 1 through n.
n is the number of heaters. i is the counter used in the summation process, adding the resistances of heater Ω1 + Ω2 + Ω3 + .… + Ωi.
When connected in parallel, the current that enters the system of heaters is split between all the heaters and shared amongst them, though not necessarily evenly.
How the current is split depends on the resistance of each heater. If the heater resistances are identical then the current is split evenly between all the heaters. Think of the water pipe analogy as the heater with higher resistance have more constricted flow, so less current goes through those heaters.
When heaters have the same resistance it’s straight-forward to determine the current passing through each one; divide the total current by the number of heaters.
In all cases of heaters connected in parallel, be there equal resistances between heaters or different resistances, the voltage across each heater will be the same.
Example:
If there are two heaters connected in parallel, each having 10Ω of resistance, then the resistance over the set of heaters is 10Ω/2 or 5Ω. If there are 16 heaters connected in parallel, each having 320Ω of resistance, then the resistance over the set of heaters is 320Ω/16 or 20Ω.
The calculation required to determine the resistance of different heater resistances connected in parallel is a bit trickier. This is where each heater offers different constricted flow in that water pipe model. It is calculated as the inverse of the sum of the inverses of the individual heater resistances.
Example:
10Ω, 20Ω and 40Ω in parallel is 1 / ( 1/10 + 1/20 + 1/40 ) = 1 / ( 0.1 + 0.05 + 0.025 ) = 1 / (0.175) ≈ 5.7Ω
Two heaters in Parallel

Three heaters in Parallel

Again, if you’re into this sort of thing, here are two formulas for determining the total resistance of a system of heaters that are connected in parallel.
If the resistances of each heater (n heaters) are the same, the total resistance of all of them connected in parallel is:
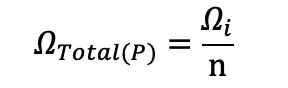
where:
ΩTotal(P) is the total resistance of heaters (n heaters) connected in parallel.
n is the number of heaters. Ωi is the resistance of an individual heater. Since they’re all the same, it can be the resistance of any one of the heaters.
If the resistances of at least one of a group of heaters (n heaters) is different, the total resistance of all of them connected in parallel is:
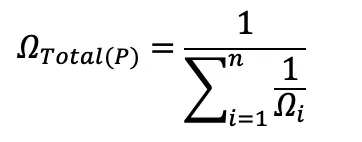
This is more work because you must calculate the sum of the inverses of each individual heater’s resistance, and then take the inverse of that when you’re done adding the inverses together.
In this formula Ωi is the resistance of the individual heaters, numbered 1 through n, like in the earlier formula. You could actually use the second formula in a scenario with all the heaters having the same resistance and you would get the same result as the first formula. It’s just a lot easier to use the first one when the resistances are all the same.
Why connect heaters in parallel? If you have a system where you can achieve the necessary process temperature without all the heaters being energized, you can operate in this fashion. If a heater fails then the remaining working heaters would have to work harder with a longer duty cycle to make up for the missing heater, but it can be done. Not all situations are good for this scenario, like if you need to heat in a very specific location or the remaining heaters just can’t pull off the work required. You would be able to see if a heater has stopped worked by either a change in the temperature profile of your system, an increase in duty cycle of the remaining heaters, or a reduction in total current drawn by the system. For some applications this works fine, for others not so much.
In conclusion, the choice between series and parallel connections depends on the specific application, required reliability, and safety considerations. While series connections ensure uniform current flow and easier fault detection, parallel setups provide greater system redundancy. Understanding the fundamental differences enables informed decisions for optimal heater performance.
