Engineering Insights
PID Temperature Controllers - What’s that About?
 As the name implies, a temperature controller’s purpose is to control a heating device so that a desired setpoint temperature (the temperature you want to achieve) is reached and maintained. A few examples of temperature controllers around your home are your central heating, refrigerator, freezer, oven, and water heater. These may be of the PID variety or could just be simple on-off controllers, otherwise known as thermostats.
As the name implies, a temperature controller’s purpose is to control a heating device so that a desired setpoint temperature (the temperature you want to achieve) is reached and maintained. A few examples of temperature controllers around your home are your central heating, refrigerator, freezer, oven, and water heater. These may be of the PID variety or could just be simple on-off controllers, otherwise known as thermostats.
For the purposes of this document, we’ll use the example of a temperature controller being used to control heating something to a certain temperature. A PID controller is more advanced than an old-fashioned wall-mounted thermostat and performs more calculations when determining how to control a process.
In the name ‘PID’, ‘P’ stands for Proportional, ‘I’ stands for Integral, and ‘D’ stands for Derivative. Does that bring anyone back to calculus class? They are all calculated to determine how to adjust the temperature of a system in order for it to achieve the setpoint temperature and hold it there. Those variables and how they are adjusted are dependent upon the current temperature being measured, the setpoint temperature, and the current rate of change of the temperature. More on that later.
A temperature controller has a temperature sensor built into it or attached to it (to sense the temperature elsewhere, away from the actual controller), that senses the temperature of the surroundings or of the process/application being heated. In the controller interface, it also has a place for the desired setpoint temperature to be entered. The difference between these two numbers determines what the controller will do, as in, turn a heater on or off.
The proportional section of a temperature controller is the easiest to understand. If the current temperature is below the desired setpoint, it turns the heater on so things can get hotter. If the current temperature is above the desired setpoint, it turns the heater off. That’s the behavior of an on-off controller when it just compares two numbers and turns things on or off. Pretty basic. That’s how an old mechanical thermostat works. There’s an issue with that type of control. As the temperature of the system approaches the setpoint temperature, the distance between the two (called the error) will decrease in size, meaning that the controller will call for less and less heat. The temperature of the system will approach the setpoint slower and slower, never really quite getting there. It will get there within a reasonable margin, but it’ll take a while to get there.
The next two methods of control (Integral and Derivative) are used to help control the temperature better and bring things where they need to be more quickly, but they introduce other issues.
Integral
The Integral part of the control reacts to the difference between the actual and setpoint temperatures as well as the time that they’re separated based on the past history of the system. You could say that this part of the control gets the system to temperature faster by looking at this error over time, but it introduces two new issues. One of the errors is overshoot, where the temperature goes beyond the setpoint temperature. The other error is hysteresis, which is a fancy word for bounce or wobble. It occurs when the temperature bounces up and down on either side of the setpoint temperature over time, which can take a while to settle down.
Derivative
The Derivative part reacts to the rate at which the other two parts of the control cause the temperature to change, regardless of how close or far away the actual temperature is from the setpoint. This can be restated as a reaction to the steepness of the temperature climb and making sure it doesn’t get too out of hand. The derivation part of the control watches the rate of change of the error of the system. It does impede the rate of change of the process (slows it down), but with the other proportional and integral components of the control, it balances out nicely, thereby reducing the overshoot and hysteresis.
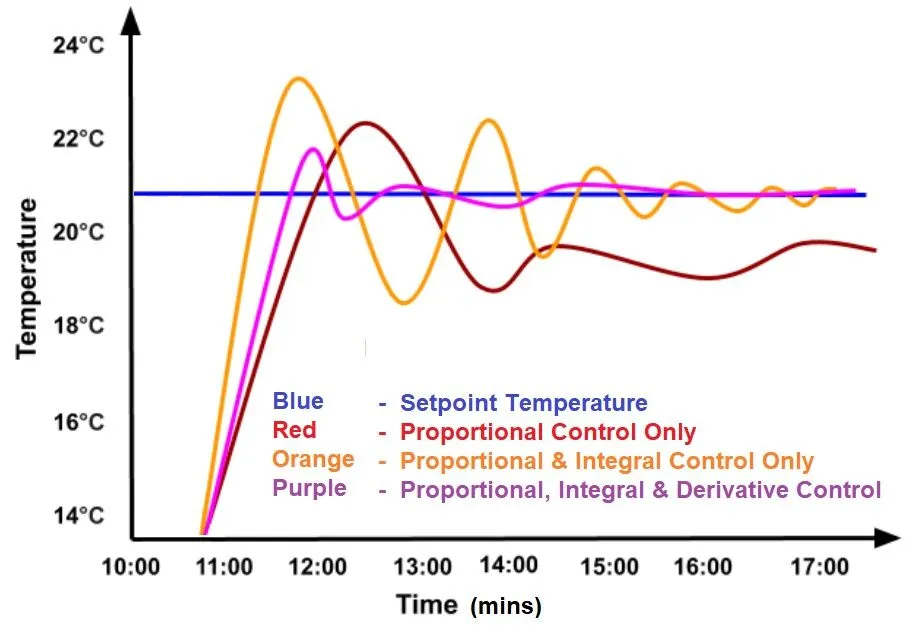
You can see in the image below how the addition of different control methods to a system improves performance.
The red line represents the simplest form of control, proportional control or on-off only. If you were to follow the red line long enough (beyond the edge of the chart) you can see how it might achieve the setpoint temperature. It’s not very good. Add the integral component of the control and you get the orange line. It introduces quite a bit of overshoot and hysteresis, but it reaches the setpoint a lot faster, though at a cost. The best line is the purple line utilizing full proportional, integral, and derivative control. The time to the setpoint is the middle of the three, but the overshoot and hysteresis are greatly lessened.
All these settings have coefficients that need to be set inside the controller. They affect how impactful each component of the input has on the behavior of the system. How on earth do you adjust the settings to get the system to behave as best as possible? You can either be a PID controller expert, or you can simply put the controller into auto mode. It’s sometimes called autotune mode. When in autotune mode, the controller will adjust the coefficients for each control input and determine how effective each of them are, adjusting as necessary. It will continue to adjust and tune the settings until it gets to optimum performance: quick ramp-up time, little overshoot, and little hysteresis (bouncing) around the setpoint temperature. This may take varying amounts of time for everything to autotune, depending on the setpoint temperature and the mass of what’s being heated. Once complete and the coefficients are set, if there are no changes to the system, those numbers don’t need to be touched again.
Something else to think about: The size and material composition of a mass being heated will determine how quickly it’ll heat up. A PID controller takes this into account and ‘watches’ the temperature and the rate at which it rises, thereby determining the best way to control the temperature. ‘Watching’ in this case means that the controller uses those three methods of control and blends them together to provide the best output to the system. They’re based on the current condition (proportional control), the past performance (integral control), and the predicted future performance based on the rate of change of the error in the system (derivative control). Once at the correct temperature, the controller will turn a heating device on and off in a fairly periodic fashion. Maybe the heater will be on 10% of the time (think of a quick blip of power, once per second, for example), or maybe the same heater would be on 90% of the time if it were heating a much larger mass, which would mean that a heater would be on for a much bigger fraction of a second.
Those differences in duty cycle (that’s what it’s called) are based on the same heater being used to heat two different masses or two masses of the same weight but of different materials (aluminum vs copper, for example). There’s another factor that can have an effect too. In the case of a cartridge heater, it would be how well it fits into a hole in the mass it’s heating, be it a tight fit or a loose, sloppy fit. For a band heater, it would be based on how tightly it’s clamped in place. A loose fit would require the heater to work harder to achieve temperature, meaning it would be on longer, take longer to reach the setpoint temperature, and once there, would have a higher duty cycle than a heater that was tightened in place well.
What this all means is that a PID temperature controller can compensate for these unideal situations in a system, be it a loose hole fit or a loosely tightened band heater. The cost, though, is heater life. The controller will make a heater work harder and hotter to achieve the desired setpoint temperature, which, though great for the system, isn’t too good when considering the longevity of a heater.
There are many uses for temperature controllers and other PID controllers in industrial applications that require the control to be precise. That’s where the PID temperature controller comes in and is able to easily provide the control needed to get processes operating smoothly. PID controllers are not just limited to heating applications. They can also be used to control the cooling of a system. Additionally, if the property of a process that needs attention can be measured and adjusted, then it can be controlled. Think of pressure, humidity, flow rates, the concentration of compounds in an air stream, and many others. They can all be controlled well with a PID controller.
